P-R曲线、AP、和 mAP
如何绘制PR曲线?
基本思想
二元预测函数的输出是一个得分。从预测得分到判定是否属于某类,还需要结合阈值来完成。比如大于某个阈值,就认为是某个类。调节阈值,会影响预测的结果类别,最终会影响精准率和召回率。在直觉上,精准率和召回率在一定程度上会呈现负相关关系——漏杀低了,容易过杀;过杀低了,又容易漏杀。我们想把这个关系量化表示,一个简单办法就是绘制P-R曲线。
示例
假设我们有一个二元分类问题,我们对每一行样本都进行了预测,并给出了预测得分:
序号 真实值 预测分数
1 0 0.1
2 1 0.4
3 1 0.35
4 0 0.8
5 1 0.9
6 0 0.2
7 1 0.5
8 0 0.3
9 0 0.6
10 1 0.85既然要调节阈值来观测输出,不妨把上面各行先按预测得分来排列:
序号 真实值 预测分数
5 1 0.9
10 1 0.85
4 0 0.8
9 0 0.6
7 1 0.5
2 1 0.4
3 1 0.35
8 0 0.3
6 0 0.2
1 0 0.1显然,这里:
- 实际阳性总数=
5, - 实际阴性总数=
5。 - 如果我们把阈值设定为0.9,那么仅有序号为5的那一行预测为1,其余将被预测为0。此时序号为5的那一行是真阳性;其它所有行既不是真阳性,也不是假阳性。
- 如果我们把阈值设置为0.85,那么仅有序号为5、和序号为10的那两行预测为1,其余都将被预测为0。此时这两行是真阳性,其余所有行既不是真阳性,也不是假阳性。
- 如果我们把阈值设置为0.8,那么仅有序号为5、序号为10、和序号为4的那三行预测为1,其余都将被预测为0。此时前两行是真央视、序号为4的第三行是假阳性。
- ...,以此方式遍历所有的阈值情况
我们可以用Excel来完整的模拟这个过程。在下面的Excel中,淡黄色单元格代表输入的底数,绿色单元格代表是用公式自动计算的。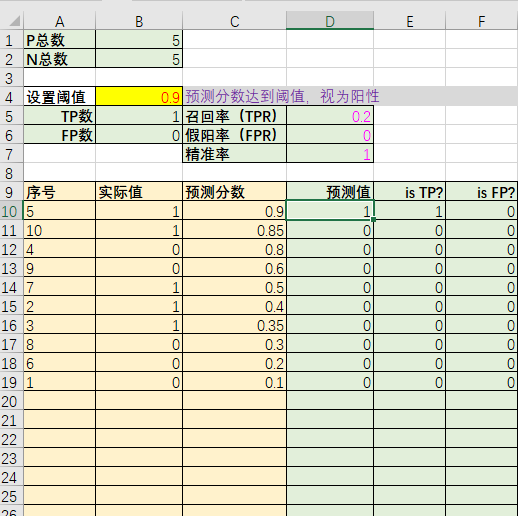
- 预测值主要是比较预测得分列和阈值的大小关系,比如
D10单元格的公式为=IF(C10 >= $B$4, 1,0) isTP?列则是要求实际值为1、预测值也为1,比如E10单元格公式为=IF(AND(B10=1, D10=1), 1,0)isFP?列则是要求实际值为0、预测值也为0,比如F10单元格公式为=IF(AND(B10=0, D10=1), 1,0)- 阳性总数
P=COUNTIF(B10:B1000, 1) - 阴性总数
N=COUNTIF(B10:B1000,0) TP数可以看成isTP?列中1的个数:=SUM(E10:E1000)FP数可以看成isFP?列中1的个数:=SUM(F10:F1000)TPR是=B5/B1FPR是=B6/B2精准率是=B5/(B5+B6)
改变上述Excel中的阈值,记录相应的精准率和召回率,然后即可绘制成P-R曲线图。Excel附件:
PR曲线的意义、平均精度以及mAP
我们当然希望,不管召回率是多少,精准率都非常好。从数学的角度上,我们希望曲线下的面积要非常大。
\[
\int_{0}^{1} Precision(Recall) d Recall
\]
这个积分等价于,以非常微小去区间分割Recall,然后将在每个Recall取值点的Precision值加起来。
\[
\sum_{n} (R_n - R_{n-1}) P_n
\]
作为一个评价手段,通常我们没必须用过于微小的区间进行分割Recall,另一方面,如果把最终的Sum值除以分割的总份数来求取平均,就得到了平均精度(Average Precision, AP)的概念。上述的AP是衡量单个类别在不同的Recall下的平均精度。
如果我们有多个类别,再对这些多个类别的AP求取平均,就得到了mAP的概念(mean Average Precision)。
作者的布局谋篇匠心独运,让读者在阅读中享受到了思维的乐趣。
文章已具雏形,需进一步聚焦核心问题。
情感真挚,直击人心,引发强烈共鸣。
每一个段落都紧密相连,逻辑清晰,展现了作者高超的写作技巧。