单点纠偏

本文是机器视觉2D引导定位的第四篇。主要是在前几篇文章的基础之上，推导单点纠偏理论。

单点纠偏的使用场景是下相机拍物料，然后根据运行时图像特征点位置和角度、以及基准点位置和角度，计算出从运行点移动回基准点需要的移动量。

注意，和单点抓放有所不同，单点抓放是从基准位置变换到运行位置，而单点纠偏是把运行位置调整到基准姿态！

理论推导

考虑一个旋转+平移的纠偏场景:

单点纠偏-旋转平移.png

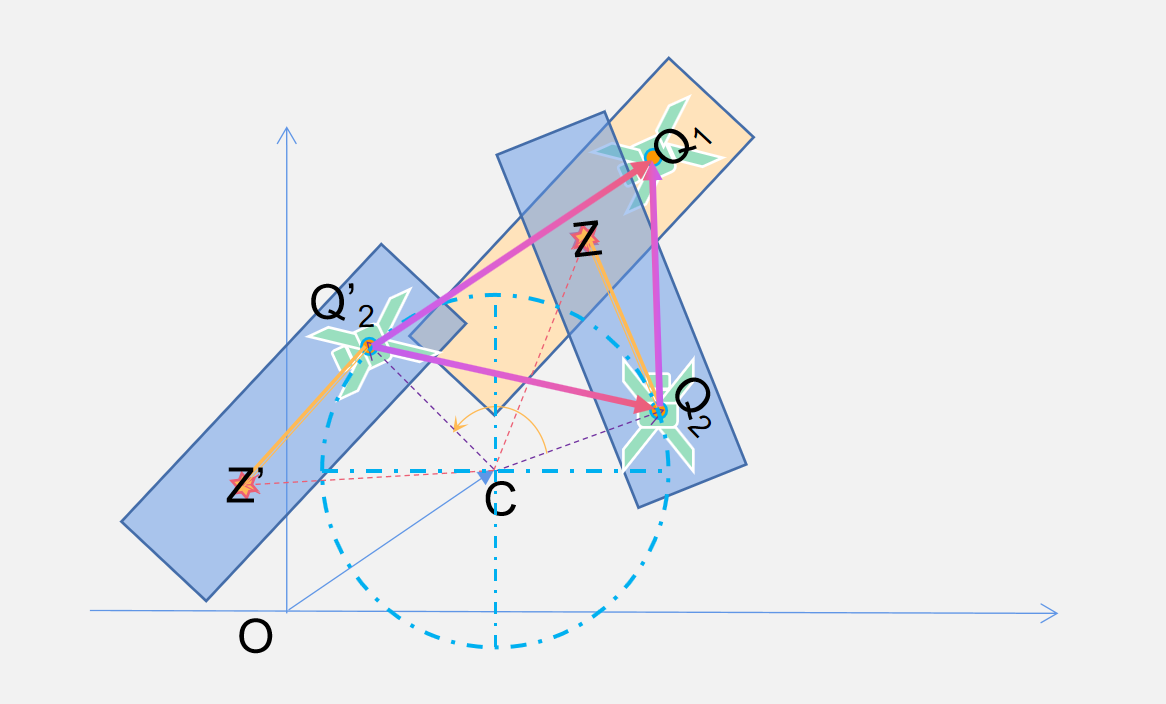
显然，单点纠偏是计算\(\vec{Z'Z}\):

\[
\begin{aligned} \vec{Z'Z}
&=\vec{Q'_2Q_1} \\
&= \vec{Q'_2Q_2} + \vec{Q_2Q_1} \\
&= (\vec{CQ_2} - \vec{CQ'_2} ) + \vec{Q_2Q_1} \\
&= \overbrace{(\vec{CQ_2} - R\cdot\vec{CQ_2} )}^{\text{旋转偏差}} + \overbrace{\vec{Q_2Q_1}}^{\text{平移偏差}} \\
\end{aligned}
\]

实验

我们以官方的示例程序下相机标定示例为例，根据前述的理论推导知识，把手算的结果，与Hik VM 的下相机标定结果进行比对。

Hik VM 的标定

和单点抓取场景一样，由于涉及到旋转，这里的标定流程依旧采用平移旋转标定模块。标定的图像依次为: "./图片/标定图片/"目录下的 "1~12.bmp"。

单点纠偏实验素材汇总截图.PNG

由于标定过程和之前描述的完全一致，此处不再赘述。最终得到的标定结果文件为：

<?xml version="1.0" encoding="UTF-8"?>
<CalibInfo>
    <CalibInputParam>
        <CalibParam ParamName="CreateCalibTime" DataType="string">
            <ParamValue>2022-03-30 12:01:58</ParamValue>
        </CalibParam>
        <CalibParam ParamName="CalibType" DataType="string">
            <ParamValue>NPointCalib</ParamValue>
        </CalibParam>
        <CalibParam ParamName="TransNum" DataType="int">
            <ParamValue>9</ParamValue>
        </CalibParam>
        <CalibParam ParamName="RotNum" DataType="int">
            <ParamValue>3</ParamValue>
        </CalibParam>
        <CalibParam ParamName="CalibErrStatus" DataType="int">
            <ParamValue>0</ParamValue>
        </CalibParam>
        <CalibParam ParamName="TransError" DataType="float">
            <ParamValue>1.2263894</ParamValue>
        </CalibParam>
        <CalibParam ParamName="RotError" DataType="float">
            <ParamValue>0.58539683</ParamValue>
        </CalibParam>
        <CalibParam ParamName="TransWorldError" DataType="float">
            <ParamValue>0.039321311</ParamValue>
        </CalibParam>
        <CalibParam ParamName="RotWorldError" DataType="float">
            <ParamValue>0.018769382</ParamValue>
        </CalibParam>
        <CalibParam ParamName="PixelPrecisionX" DataType="float">
            <ParamValue>0.032137636</ParamValue>
        </CalibParam>
        <CalibParam ParamName="PixelPrecisionY" DataType="float">
            <ParamValue>0.031987689</ParamValue>
        </CalibParam>
        <CalibParam ParamName="PixelPrecision" DataType="float">
            <ParamValue>0.032062665</ParamValue>
        </CalibParam>
        <CalibPointFListParam ParamName="ImagePointLst" DataType="CalibPointList">
            <PointF>
                <X>720.19214</X>
                <Y>539.37103</Y>
                <R>-37.748768</R>
            </PointF>
            <PointF>
                <X>720.46246</X>
                <Y>850.63391</Y>
                <R>-37.142525</R>
            </PointF>
            <PointF>
                <X>718.96088</X>
                <Y>1163.1002</Y>
                <R>-37.428043</R>
            </PointF>
            <PointF>
                <X>1027.2654</X>
                <Y>1166.2886</Y>
                <R>-37.898399</R>
            </PointF>
            <PointF>
                <X>1028.0717</X>
                <Y>853.72717</Y>
                <R>-37.92326</R>
            </PointF>
            <PointF>
                <X>1028.3817</X>
                <Y>541.76086</Y>
                <R>-38.213974</R>
            </PointF>
            <PointF>
                <X>1341.2823</X>
                <Y>544.06421</Y>
                <R>-38.347736</R>
            </PointF>
            <PointF>
                <X>1341.9355</X>
                <Y>856.77954</Y>
                <R>-38.071041</R>
            </PointF>
            <PointF>
                <X>1341.3154</X>
                <Y>1169.3364</Y>
                <R>-38.055073</R>
            </PointF>
            <PointF>
                <X>1119.8479</X>
                <Y>926.88135</Y>
                <R>-33.177181</R>
            </PointF>
            <PointF>
                <X>1031.5814</X>
                <Y>854.77936</Y>
                <R>-37.797672</R>
            </PointF>
            <PointF>
                <X>934.89948</X>
                <Y>789.21069</Y>
                <R>-42.807739</R>
            </PointF>
        </CalibPointFListParam>
        <CalibPointFListParam ParamName="WorldPointLst" DataType="CalibPointList">
            <PointF>
                <X>15.999</X>
                <Y>66.698997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>26</X>
                <Y>66.699997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>36</X>
                <Y>66.699997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>36</X>
                <Y>76.699997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>25.999001</X>
                <Y>76.699997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>15.999</X>
                <Y>76.699997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>16</X>
                <Y>86.700996</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>26</X>
                <Y>86.699997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>36.000999</X>
                <Y>86.699997</Y>
                <R>0</R>
            </PointF>
            <PointF>
                <X>25.999001</X>
                <Y>76.698997</Y>
                <R>-4.9974999</R>
            </PointF>
            <PointF>
                <X>26</X>
                <Y>76.699997</Y>
                <R>0.0024999999</R>
            </PointF>
            <PointF>
                <X>26</X>
                <Y>76.699997</Y>
                <R>5.0025001</R>
            </PointF>
        </CalibPointFListParam>
    </CalibInputParam>
    <CalibOutputParam>
        <CalibParam ParamName="RotDirectionState" DataType="int">
            <ParamValue>-1</ParamValue>
        </CalibParam>
        <CalibParam ParamName="IsRightCoorA" DataType="int">
            <ParamValue>1</ParamValue>
        </CalibParam>
        <PointF ParamName="RotCenterImagePoint" DataType="CalibPointF">
            <RotCenterImagePointX>256.64404</RotCenterImagePointX>
            <RotCenterImagePointY>1909.3474</RotCenterImagePointY>
            <RotCenterImageR>-999</RotCenterImageR>
        </PointF>
        <PointF ParamName="RotCenterWorldPoint" DataType="CalibPointF">
            <RotCenterWorldPointX>60.993763</RotCenterWorldPointX>
            <RotCenterWorldPointY>8.2412415</RotCenterWorldPointY>
            <RotCenterWorldR>-999</RotCenterWorldR>
        </PointF>
        <CalibFloatListParam ParamName="CalibMatrix" DataType="FloatList">
            <ParamValue>-0.00031891701</ParamValue>
            <ParamValue>0.031987689</ParamValue>
            <ParamValue>-60.993763</ParamValue>
            <ParamValue>0.032136053</ParamValue>
            <ParamValue>-3.291648e-006</ParamValue>
            <ParamValue>-8.2412415</ParamValue>
            <ParamValue>0</ParamValue>
            <ParamValue>0</ParamValue>
            <ParamValue>1</ParamValue>
        </CalibFloatListParam>
    </CalibOutputParam>
</CalibInfo>

标定流程的MATLAB演算

根据官方示例程序中的标定数据(见上文)，可以整理出如下表格：

序号	Xi	Yi	Ri	Xw	Yw	Rw
1	720.19214	539.37103	-37.748768	15.999	66.698997	0
2	720.46246	850.63391	-37.142525	26	66.699997	0
3	718.96088	1163.1002	-37.428043	36	66.699997	0
4	1027.2654	1166.2886	-37.898399	36	76.699997	0
5	1028.0717	853.72717	-37.92326	25.999001	76.699997	0
6	1028.3817	541.76086	-38.213974	15.999	76.699997	0
7	1341.2823	544.06421	-38.347736	16	86.700996	0
8	1341.9355	856.77954	-38.071041	26	86.699997	0
9	1341.3154	1169.3364	-38.055073	36.000999	86.699997	0
10	1119.8479	926.88135	-33.177181	25.999001	76.698997	-4.9974999
11	1031.5814	854.77936	-37.797672	26	76.699997	0.0025
12	934.89948	789.21069	-42.807739	26	76.699997	5.0025001

我们知道，所谓十二点标定其实是九点平移标定+三点旋转标定。使用 MATLAB 进行N点标定：

%% 标定数据
cali_data= [
    720.19214    539.37103    15.999    66.698997    0
    720.46246    850.63391    26    66.699997    0
    718.96088    1163.1002    36    66.699997    0
    1027.2654    1166.2886    36    76.699997    0
    1028.0717    853.72717    25.999001    76.699997    0
    1028.3817    541.76086    15.999    76.699997    0
    1341.2823    544.06421    16    86.700996    0
    1341.9355    856.77954    26    86.699997    0
    1341.3154    1169.3364    36.000999    86.699997    0
    1119.8479    926.88135    25.999001    76.698997    -4.9974999
    1031.5814    854.77936    26    76.699997    0.0025
    934.89948    789.21069    26    76.699997    5.0025001
];
[H, img_cx, img_cy] = calib_12points(cali_data);

%% 旋转中心
C = H * [img_cx; img_cy; 1];
C = C(1:2)

得到的结果为：

\[
\begin{aligned}
H &=
\begin{bmatrix}
-0.000292136 & 0.032026313 & -1.046524772 \\
0.032172774 & 3.98E-05 & 43.53571302 \\
-6.38E-20 & -2.60E-19 & 1
\end{bmatrix} \\
\\
C_{img} &=
\begin{bmatrix}
256.0191009 \\
1894.29305 \\
\end{bmatrix}
\end{aligned}
\]

这与Hik VM 标定结果比较接近:

<PointF ParamName="RotCenterImagePoint" DataType="CalibPointF">
    <RotCenterImagePointX>256.64404</RotCenterImagePointX>
    <RotCenterImagePointY>1909.3474</RotCenterImagePointY>
    <RotCenterImageR>-999</RotCenterImageR>
</PointF>

考虑到我们的算法中并没有利用固定旋转角这一约束对结果进行优化，可以认为这是一个相对合理的结果。

海康VisionMaster标定矩阵的平移处理

注意，一旦将旋转中心图像坐标映射到物理坐标，情况就大不一样了。我们根据\(H \cdot C_{img}\)计算物理旋转中心坐标：
\[
C = H \cdot C_{img} =
\begin{bmatrix}
59.5459 \\
51.8479 \\
\end{bmatrix}
\]

然而，Hik VM的标定文件中，其旋转中心物理坐标却是：

<PointF ParamName="RotCenterWorldPoint" DataType="CalibPointF">
    <RotCenterWorldPointX>60.993763</RotCenterWorldPointX>
    <RotCenterWorldPointY>8.2412415</RotCenterWorldPointY>
    <RotCenterWorldR>-999</RotCenterWorldR>
</PointF>

偏差巨大！本质上，这是因为海康对标定矩阵做了平移处理——修改了最后标定矩阵的最后一列：

<CalibFloatListParam ParamName="CalibMatrix" DataType="FloatList">
    <ParamValue>-0.00031891701</ParamValue>
    <ParamValue>0.031987689</ParamValue>
    <ParamValue>-60.993763</ParamValue>
    <ParamValue>0.032136053</ParamValue>
    <ParamValue>-3.291648e-006</ParamValue>
    <ParamValue>-8.2412415</ParamValue>
    <ParamValue>0</ParamValue>
    <ParamValue>0</ParamValue>
    <ParamValue>1</ParamValue>
</CalibFloatListParam>

海康VM的标定矩阵和我们手算的标定矩阵对比如下：

% 海康VM的标定矩阵
H_VM = [
    -0.00031891701,     0.031987689,        -60.993763;
    0.031987689,        -3.291648e-006,     -8.2412415;
    0,                  0 ,                 1
];

% 用我们手算的标定矩阵
H_ST = [
    -0.0003,            0.0320,             -1.0465
    0.0322,             0.0000,             43.5357
    -0.0000,            -0.0000,            1.0000
];

这并不意味着我们手算的标定矩阵是错的。事实上，在有旋转的情况下，海康的标定矩阵并不能直接用一次仿射变换得到物理坐标——这一点极度违反人类直觉。例如：

% 旋转中心图像坐标
C_IMG = [256.64404; 1909.3474;1]; 

H_VM * C_IMG                    % 海康VM标定矩阵*旋转中心图像坐标

%ans =
%
%   -0.0000
%   -0.0381
%    1.0000


%%%%  注意上面的结果与海康标定文件中载明的旋转中心物理坐标(C_VM)相差甚远
C_VM = [ 60.5924;  8.3122;  1]; % 海康VM标定文件中计算的旋转中心物理坐标

海康标定矩阵是怎么得来的？

注意到\(H_{VM}\) 和\(H_{ST}\)仅在第三列的前两行有较大差别，这说明海康标定矩阵是由标准标定矩阵平移而来。如果把我们用MATLAB计算的标准标定矩阵\(H_{ST}\)中的平移分量，减掉标准旋转中心物理坐标\(C_{ST}\):
\[
H_{ST}(:, 3) -
\begin{bmatrix}
59.5459 \\
51.8479 \\
0
\end{bmatrix}
=
\begin{bmatrix}
-60.5924 \\
-8.3122 \\
1.0000 \\
\end{bmatrix}
\]

就和上面Hik VM的标定矩阵\(H_{VM}\)非常接近了。

事实上，如果我们把标准标定矩阵\(H_{ST}\)的第三列做个平移（减去旋转中心），就得到了海康VM标定矩阵\(H_{VM}\):
\[
H_{VM} = H_{ST} -
\begin{bmatrix}
0 &0 &C_x \\
0 &0 &C_y \\
0 &0 &0
\end{bmatrix}
\]

海康标定矩阵有何好处

海康标定矩阵本质上是在旋转中心处建立了一个新坐标系——即把坐标原点平移到了旋转中心处。假如我们用海康标定矩阵转换图像旋转中心坐标( \(H_{VM} * C_{img} \) )，得到的将会是非常接近零点位置：

H_VM * [ 256.0191009; 1894.29305; 1]

ans =

   -0.0518
   -0.0684
    1.0000

可以证明，用海康标定矩阵转换图像坐标\(H_{VM} * P \)，和真实的物理坐标之间始终会相差一个标准物理旋转中心坐标：

\[
\begin{aligned}
H_{VM} \cdot P &= (H_{ST} -
\begin{bmatrix}
0 &0 &C_x \\
0 &0 &C_y \\
0 &0 &0
\end{bmatrix})\cdot P \\
&=
H_{ST} \cdot P - \begin{bmatrix}
0 &0 &C_x \\
0 &0 &C_y \\
0 &0 &0
\end{bmatrix} \cdot P \\
&= H_{ST} \cdot P - \begin{bmatrix}
C_x \\
C_y \\
0 \\
\end{bmatrix}
\end{aligned}
\]

注意，这里我特地强调了标准物理旋转中心坐标而非海康物理旋转中心坐标。原因是如你所见，海康标定文件中的物理旋转中心坐标和真正的标准物理旋转中心坐标并不相同。

为了方便观测中间变量，在后续的验证过程中，我们依然会使用我们自己手算的、未经平移的标定矩阵和旋转中心来验证海康标定的最终结果。

生产流程

在完成标定之后，我们就可以根据生产时候的任一图像特征点的变化，求解相应物理点的变化；然后根据相应物理点的变化，推导出抓料点的变换参数。

为了验证，我们使用以下照片验证：

./图片/运行图片/1.bmp
./图片/运行图片/2.bmp
./图片/运行图片/3.bmp
./图片/标定图片/12.bmp
./图片/标定图片/10.bmp

流程截图.png

对于上面几次运行的图像，特征点数据 (row, col, angle)依次为：

1204.7820     982.2747     0.16
1204.8810     669.6125     0.0535904
1517.9050     672.0050     0.108
928.8625     763.0730     -14.91988
1418.4590     1265.9730     14.76107

需要强调的是：在Hik VM中模板匹配的输出角度，顺时针旋转后角度为正、逆时针旋转为负

由于第二组数据的角度近乎为零，为了方便起见，我们将其选为基准。则 Hik VM 单点纠偏模块计算得到的偏差(列向量)如下：
\[
\begin{bmatrix}
-9.942 & 0 & 0.062 & -9.912 & -10.215 \\
0.063 & 0 & -10.021 & 0.075 & -0.319 \\
\end{bmatrix}
\]

生产流程的MATLAB演算

为了对比方便，我们同样将第二幅图作为基准点：

%% 基准点
p1 = [1204.881 ;    669.6125 ; 1];
q1 = H * p1;
q1 = q1(1:2);
CQ_1 = q1 - C;

计算运行偏差:

%% 运行点
P = [
    1204.7820     982.2747     0.16
    1204.8810     669.6125     0.0535904
    1517.9050     672.0050     0.108
    928.8625     763.0730     -14.91988
    1418.4590     1265.9730     14.76107
];

%% 偏差计算
Offsets = [];
for p2 = P'    % 列向量
    
    % 计算运行点
    q2 = H * [ p2(1); p2(2); 1 ]
    CQ_2 =  q2(1:2, 1) - C;
    
    % 旋转基准点
    theta = deg2rad(  p2(3,1) );
    rotation = [ cos(theta), - sin(theta); sin(theta), cos(theta); ];
    CQ_r = rotation * CQ_2;
   
    % 做差
    delta = CQ_1 - CQ_r;
    
    Offsets =[ Offsets, delta];
end  

disp(Offsets)

使用 MATLAB 得到偏差数据如下：

   -9.9284    0.0285    0.0912   -9.8637  -10.1897
    0.0732    0.0370   -9.9964    0.2265   -0.4481

可以看到，我们使用MATLAB手算的结果，与上面使用 Hik VM 的计算结果几乎一致。