单点抓放实践——使用Hik VisionMaster和MATLAB进行交叉验证

本文是机器视觉2D引导定位的第三篇。主要是基于前两篇的理论，使用 Hik VM 进行实践，计算旋转平移标定的偏移量，并与MATLAB手算的结果进行比对。

过程简介

计算仿射变换矩阵
计算旋转中心
注册基准点
计算运行点与基准点的变换参数

在实操上，体现为标定和生产两个流程：

VM生产流程截图.png

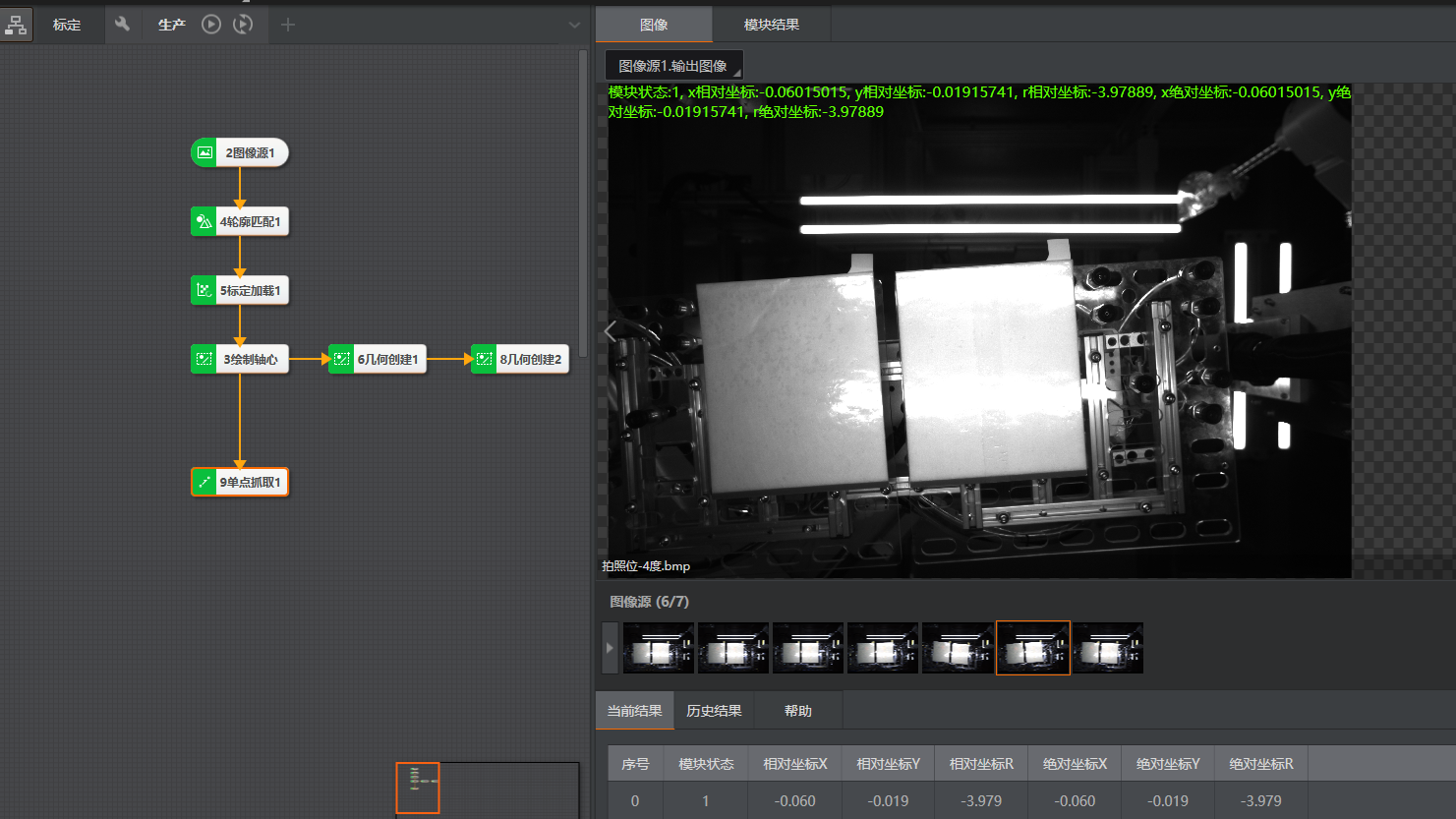
Hik VM 标定与运行

标定

采集图像过程如下：

九点标定（计算标定矩阵），采集九张图像，同时记录物理坐标
在基准拍照位进行五点拟圆（计算旋转中心），采集五张图像，同时记录物理坐标

单点抓取实验素材汇总截图.PNG

Hik VM标定出标定矩阵和旋转中心为：

<?xml version="1.0" encoding="UTF-8"?>
<CalibInfo>
    <CalibInputParam>
        <CalibParam ParamName="CreateCalibTime" DataType="string">
            <ParamValue>2023-06-12 14:22:42</ParamValue>
        </CalibParam>
        <CalibParam ParamName="CalibType" DataType="string">
            <ParamValue>NPointCalib</ParamValue>
        </CalibParam>
        <CalibParam ParamName="CameraMode" DataType="int">
            <ParamValue>CameraStatic</ParamValue>
        </CalibParam>
        <CalibParam ParamName="TransNum" DataType="int">
            <ParamValue>9</ParamValue>
        </CalibParam>
        <CalibParam ParamName="RotNum" DataType="int">
            <ParamValue>3</ParamValue>
        </CalibParam>
        <CalibParam ParamName="CalibErrStatus" DataType="int">
            <ParamValue>0</ParamValue>
        </CalibParam>
        <CalibParam ParamName="TransError" DataType="float">
            <ParamValue>0.61861861</ParamValue>
        </CalibParam>
        <CalibParam ParamName="RotError" DataType="float">
            <ParamValue>0.089774422</ParamValue>
        </CalibParam>
        <CalibParam ParamName="TransWorldError" DataType="float">
            <ParamValue>0.078114673</ParamValue>
        </CalibParam>
        <CalibParam ParamName="RotWorldError" DataType="float">
            <ParamValue>0.011336063</ParamValue>
        </CalibParam>
        <CalibParam ParamName="PixelPrecisionX" DataType="float">
            <ParamValue>0.12673379</ParamValue>
        </CalibParam>
        <CalibParam ParamName="PixelPrecisionY" DataType="float">
            <ParamValue>0.12581174</ParamValue>
        </CalibParam>
        <CalibParam ParamName="PixelPrecision" DataType="float">
            <ParamValue>0.12627275</ParamValue>
        </CalibParam>
        <CalibPointFListParam ParamName="ImagePointLst" DataType="CalibPointList">
            <PointF>
                <X>1672.585</X>
                <Y>2306.25</Y>
                <R>0.016084053</R>
            </PointF>
            <PointF>
                <X>1671.593</X>
                <Y>2146.552</Y>
                <R>0.065511368</R>
            </PointF>
            <PointF>
                <X>1671.401</X>
                <Y>1989.853</Y>
                <R>0.096516043</R>
            </PointF>
            <PointF>
                <X>1512.703</X>
                <Y>1990.172</Y>
                <R>0.059072878</R>
            </PointF>
            <PointF>
                <X>1513.178</X>
                <Y>2148.7661</Y>
                <R>-0.026686637</R>
            </PointF>
            <PointF>
                <X>1513.7321</X>
                <Y>2306.6699</Y>
                <R>-0.034523372</R>
            </PointF>
            <PointF>
                <X>1356.887</X>
                <Y>2308.7781</Y>
                <R>-0.074267119</R>
            </PointF>
            <PointF>
                <X>1356.167</X>
                <Y>2149.814</Y>
                <R>-0.027513284</R>
            </PointF>
            <PointF>
                <X>1355.734</X>
                <Y>1990.894</Y>
                <R>0.07842128</R>
            </PointF>
            <PointF>
                <X>1513.2841</X>
                <Y>2148.7141</Y>
                <R>-0.030053759</R>
            </PointF>
            <PointF>
                <X>1501.818</X>
                <Y>2168.0769</Y>
                <R>-1.9821</R>
            </PointF>
            <PointF>
                <X>1526.124</X>
                <Y>2129.0259</Y>
                <R>2.026149</R>
            </PointF>
        </CalibPointFListParam>
        <CalibPointFListParam ParamName="WorldPointLst" DataType="CalibPointList">
            <PointF>
                <X>108.21</X>
                <Y>-687.41998</Y>
                <R>0.016000001</R>
            </PointF>
            <PointF>
                <X>88.220001</X>
                <Y>-687.41998</Y>
                <R>0.066</R>
            </PointF>
            <PointF>
                <X>68.230003</X>
                <Y>-687.41998</Y>
                <R>0.097000003</R>
            </PointF>
            <PointF>
                <X>68.239998</X>
                <Y>-667.44</Y>
                <R>0.059</R>
            </PointF>
            <PointF>
                <X>88.209999</X>
                <Y>-667.40002</Y>
                <R>-0.027000001</R>
            </PointF>
            <PointF>
                <X>108.24</X>
                <Y>-667.40002</Y>
                <R>-0.035</R>
            </PointF>
            <PointF>
                <X>108.24</X>
                <Y>-647.40997</Y>
                <R>-0.074000001</R>
            </PointF>
            <PointF>
                <X>88.239998</X>
                <Y>-647.40997</Y>
                <R>-0.028000001</R>
            </PointF>
            <PointF>
                <X>68.239998</X>
                <Y>-647.40997</Y>
                <R>0.078000002</R>
            </PointF>
            <PointF>
                <X>88.209999</X>
                <Y>-667.40002</Y>
                <R>-0.029999999</R>
            </PointF>
            <PointF>
                <X>88.209999</X>
                <Y>-667.40002</Y>
                <R>-1.982</R>
            </PointF>
            <PointF>
                <X>88.209999</X>
                <Y>-667.40002</Y>
                <R>2.026</R>
            </PointF>
        </CalibPointFListParam>
    </CalibInputParam>
    <CalibOutputParam>
        <CalibParam ParamName="RotDirectionState" DataType="int">
            <ParamValue>-999</ParamValue>
        </CalibParam>
        <CalibParam ParamName="IsRightCoorA" DataType="int">
            <ParamValue>1</ParamValue>
        </CalibParam>
        <PointF ParamName="RotCenterImagePoint" DataType="CalibPointF">
            <RotCenterImagePointX>2066.9048</RotCenterImagePointX>
            <RotCenterImagePointY>2496.908</RotCenterImagePointY>
            <RotCenterImageR>-999</RotCenterImageR>
        </PointF>
        <PointF ParamName="RotCenterWorldPoint" DataType="CalibPointF">
            <RotCenterWorldPointX>316.02301</RotCenterWorldPointX>
            <RotCenterWorldPointY>-260.5065</RotCenterWorldPointY>
            <RotCenterWorldR>-999</RotCenterWorldR>
        </PointF>
        <CalibFloatListParam ParamName="CalibMatrix" DataType="FloatList">
            <ParamValue>0.00091244816</ParamValue>
            <ParamValue>0.12581043</ParamValue>
            <ParamValue>-316.02301</ParamValue>
            <ParamValue>-0.1267305</ParamValue>
            <ParamValue>0.00057405682</ParamValue>
            <ParamValue>260.5065</ParamValue>
            <ParamValue>0</ParamValue>
            <ParamValue>0</ParamValue>
            <ParamValue>1</ParamValue>
        </CalibFloatListParam>
    </CalibOutputParam>
</CalibInfo>

对于单点抓取模块，如果我们只关心相对于基准位置的偏移量、而不关心抓件的绝对物理坐标，则示教物理点可以填0：

单点抓取-配置信息.png

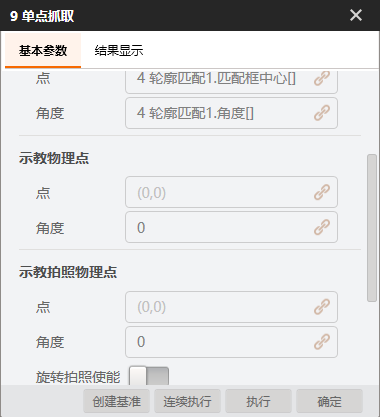
备注：绝对坐标（X,Y,R）为机构抓取的绝对物理位置，即相对坐标加上示教物理点

如果每次拍照姿态固定，则示教拍照物理点也可填0。

我们选取7张图片进行测试，其图像特征运行点参数(row, col, angle)分别为：
\[
\begin{bmatrix}
1644.710 &2184.197 &0.00374 \\
1683.809 &2183.948 &0.01197 \\
1683.809 &2144.769 &0.00008 \\
1671.944 &2158.424 &-1.97127 \\
1718.255 &2109.892 &5.39912 \\
1660.219 &2172.890 &-3.97881 \\
1696.335 &2131.415 &2.02432 \\
\end{bmatrix}
\]

最终 Hik VM 给出的偏差，以列向量的形式分别为：
\[
\begin{bmatrix}
4.928005 &4.939564 &0 &-0.03858948 &0.1443291 &0.06015015 &0.06814575 \\
4.980583 &0.03192139 &0 &-0.01818466 &0.1011848 &0.01915741 &0.0371885 \\
\end{bmatrix}
\]

使用MATLAB交叉验证

和 Hik VM 一样，我们采取九点标定法计算仿射变换矩阵；而和 Hik VM 不一样的是，为了更准确的计算旋转中心，我们采取五点共圆拟合法，故这里要给出5组旋转轨迹点。

%% 标定数据
cali_data= [
    1672.585    2306.25    108.21    -687.42    0
    1671.593    2146.552    88.22    -687.42    0
    1671.401    1989.853    68.23    -687.42    0
    1512.703    1990.172    68.24    -667.44    0
    1513.178    2148.766    88.21    -667.4    0
    1513.732    2306.67    108.24    -667.4    0
    1356.887    2308.778    108.24    -647.41    0
    1356.167    2149.814    88.24    -647.41    0
    1355.734    1990.894    68.24    -647.41    0
    1548.621    2097.044    88.21    -667.4    5.3
    1513.284    2148.714    88.21    -667.4    0
    1490.558    2188.755    88.21    -667.4    -4
    1513.284    2148.714    0    0    0
    1501.818    2168.077    0    0    0
    1548.621    2097.044    0    0    0
    1490.558    2188.755    0    0    0
    1526.214    2129.026    0    0    0
];
[H, img_cx, img_cy] = calib_12points(cali_data);

%% 旋转中心
C = H * [img_cx; img_cy; 1];
C = C(1:2)

如果你仔细观察的话，会发现这里的 \(H\) 和海康VisionMaster的标定矩阵在第三列上有较大差异。这一点并不影响我们用MATLAB进行最终结果的验证。为了不一次性引入过多细节，我们会在下一篇《单点纠偏》文章中，再仔细讲解海康VisionMaster标定矩阵和标准标定矩阵的差异。

注册基准点：

%% 基准点
p1 = [1683.809 ;  2144.769 ; 1];
q1 = H * p1;
q1 = q1(1:2);
CQ_1 = q1 - C;

运行点偏差计算：

%% 运行点
P = [
    1644.710     2184.197     0.00374
    1683.809     2183.948     0.01197
    1683.809     2144.769     0.00008
    1671.944     2158.424     -1.97127
    1718.255     2109.892     5.39912
    1660.219     2172.890     -3.97881
    1696.335     2131.415     2.02432
];

%% 偏差计算
Offsets = [];
for p2 = P'    % 列向量
    
    % 计算运行点
    q2 = H * [ p2(1); p2(2); 1 ]
    CQ_2 =  q2(1:2, 1) - C;
    
    % 旋转基准点
    theta = deg2rad(  p2(3,1) );
    rotation = [ cos(theta), - sin(theta); sin(theta), cos(theta); ];
    CQ_r = rotation * CQ_1;
   
    % 做差
    delta = CQ_2 - CQ_r;
    
    Offsets =[ Offsets, delta];
end  

disp(Offsets)

最终输出结果为：

    4.9455    4.9544    0.0001   -0.0477    0.1710   -0.0780    0.0780
    4.9789    0.0287    0.0001   -0.0122    0.0875   -0.0066    0.0316

可以看到，我们这里使用 MATLAB 手算的结果，与上面 Hik VM 的计算结果非常接近。

单点抓放实践——使用Hik VisionMaster和MATLAB进行交叉验证

过程简介

Hik VM 标定与运行

标定

使用MATLAB交叉验证

添加新评论

最新文章

最近回复

分类

归档

其它