基底变换

问题

考虑空间中有一个固定的点\(\vec{u}\)。现在建立一套坐标系\(A\)，在坐标系\(A\)中，\(\vec{u}\)可以表示成\(\alpha_1 \vec{a_1} + ... + \alpha_n \vec{a_ n}\)。

现在坐标系\(A\)之外，再另建一套坐标系\(B\)，基底是\(\vec{b_1}\), ... , \(\vec{b_n}\)，问如何求点\(\vec{u}\)在\(B\)里的坐标？

记号和术语

由于涉及多套坐标系的转换，我们引入记号\([\vec{u}]_A\)表示向量\(\vec{u}\)在坐标系\(A\)下的各基向量的线性组合。

注意，\([\vec{u}]_A\)和\([\vec{u}]_B\)本质上描述的是同一个向量对象，你可以理解成我们在不同坐标系下为同一个物理点其起了不同的名字。

另一方面，从\([\vec{u}]_A\)到\([\vec{u}]_B\)，其实是用另一套基向量来描述同一个的\(\vec{u}\)。这称之为基底变换，可以证明基底变换是一种线性变换（符合线性叠加原理）。

基底变换公式

显然，由于\(\vec{u}=\alpha_1 \vec{a_1} + ... + \alpha_n \vec{a_ n}\)，我们将其带入\([\vec{u}]_B\)得到：
\[
[\vec{u}]_B = [\alpha_1\vec{a}_1 + ... + \alpha_2 \vec{a}_2 ]_B
\]

由于基底变换是一个线性变换，根据叠加原理，我们可以针对各个分量单独变换最后再叠加，所以
\[
[\vec{u}]_B = [\alpha_1\vec{a}_1]_B + ... + [\alpha_2 \vec{a}_2 ]_B \\
\Rightarrow
[\vec{u}]_B = \alpha_1 [\vec{a}_1]_B + ... + \alpha_2 [\vec{a}_2 ]_B
\]

写成矩阵形式：
\[
[\vec{u}]_B =
\begin{bmatrix}
[\vec{a}_1]_B & ... & [\vec{a}_n ]_B
\end{bmatrix}
\begin{bmatrix}
\alpha_1 \\ ... \\ \alpha_n
\end{bmatrix}
\]
显然，\(\alpha_1, ... , \alpha_n\)是\(\vec{u}\)在\(A\)下的坐标，故有：

\[
[\vec{u}]_B= P_{B \leftarrow A} [\vec{u}]_A
\]

其中\(P_{B \leftarrow A}\)表示一个的基底变换矩阵：
\[
P_{B \leftarrow A} = [ [\vec{a}_1]_B , ... , [\vec{a}_n ]_B ]
\]
\(P_{B \leftarrow A}\)的每列都对应\(A\)的基向量在\(B\)下的表达。

示例

考虑在xOy坐标系A中，两个坐标轴的单位向量分别是\(\vec{i}\) 和 \(\vec{j}\)。其中有一个点P(1,3)，用向量表示为 \(\vec{u} = 1 \vec{i}+ 3 \vec{j}\)。

现在有一个新坐标系B，其方向向量分别是\(\vec{m}\) 和\(\vec{n}\)，其中\(\vec{n}\)和\(\vec{j}\)重合。问：P在坐标系B中的坐标是多少？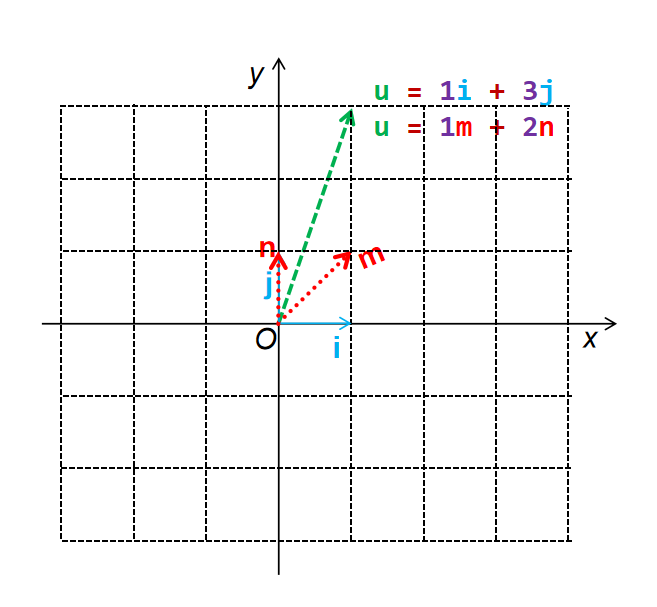

根据上面的公式，\(\vec{i}\) 在坐标系B中可以表示成 \( 1 \vec{m} - 1 \vec{n} \), 而\(\vec{j}\) 在坐标系B中可以表示成 \( 0 \vec{m} + 1 \vec{n} \)。所以：
\[
P_{B \leftarrow A} =
\begin{bmatrix}
1 & 0 \\
-1 & 1
\end{bmatrix}
\]

所以，坐标系B中，P点坐标是：
\[
\begin{bmatrix}
1 & 0 \\
-1 & 1
\end{bmatrix}
\begin{bmatrix}
1 \\
3
\end{bmatrix} =
\begin{bmatrix}
1 \\
2
\end{bmatrix}
\]

有平移的情况

我们知道，平移并不是线性变换。为了用线性变换（矩阵乘法）来表达平移，我们可以引起齐次坐标来实现。原来的二维坐标\( \begin{bmatrix} x \\ y \end{bmatrix} \) 将变成三维: \( \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \) , 相应的\(P_{B \leftarrow A}\)将变成一个 \( 3 \times 3 \)的矩阵，其中：

• 第一列 \( \begin{bmatrix} m_{11} \\ m_{21} \\ 0 \end{bmatrix} \) 表示原x轴单位向量在新坐标系中的表示；
• 第一列 \( \begin{bmatrix} m_{11} \\ m_{21} \\ 0 \end{bmatrix}\) 表示原y轴单位向量在新坐标系中的表示；
• 第三列 \( \begin{bmatrix} t_x \\ t_y \\ 1 \end{bmatrix} \) 表示从坐标系A的原点平移到坐标系B的原点的位置。

链式转换规则

对于两个坐标系的坐标转换，可以用公式\([\vec{u}]_B= P_{B \leftarrow A} [\vec{u}]_A\)表达。假如我们有多个个坐标系，显然就可以链式转换：
\[
[\vec{u}]_C= P_{C \leftarrow B} [\vec{u}]_B \\
\Rightarrow
[\vec{u}]_C = P_{C \leftarrow B}
P_{B \leftarrow A} [\vec{u}]_A
\]